D.Palasro's Blog: Profil Kecepatan dan Hambatan dari Aliran Laminar di atas Sebuah Plat (Take Home UTS Komputasi Teknik)

Konservasi Massa

Pada kondisi ini, kecepatan u searah sumbu x sehingga tidak ada aliran melintasinya. Fungsi aliran

Persamaan kontuinitas aliran dua dimensi adalah

Fluida bergerak dengan kecepatan seragam u_∞ pada arah x, u= u_∞dan v=0. Sehingga:

Kemudian diintegralkan,

Bandingkan kedua persamaan di atas, kita dapatkan fn(x) = constant dan fn(y)= u_∞y + constant , sehingga

Jika kita tetapkan constant=0 maka persamaan fungsi aliran

Konservasi Momentum

Pernyataan dasar konservasi momentum arah sumbu x adalah

Tegangan geser dapat dihilangkan dengan bantuan Hukum Newton viskositas geser

Sehingga persamaan momentum menjadi

Jika kondisi dibatasi dengan ρ≈constant dan μ≈constant , maka persamaan menjadi

Persamaan di atas adalah salah satu bentuk persamaan momentum lapisan batas incompressible dua dimensi

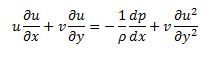
Perkiraan lapisan batas dari persamaan di atas adalah

|∂u/∂x| pada umumnya << |∂u/∂y|
v pada umumnya << u
p≠ fn(y)

Persamaan Bernoulli untuk aliran bebas sedikit di atas lapisan batas di mana tidak ada viskositas geser

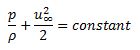
Dapat diturunkan untuk menghilangkan gradien tekanan

Persamaan momentum menjadi

Jika tidak ada gradient tekanan di dalam aliran-jika p, u_∞konstan ketika melewati sebuah plat- maka persamaan momentum menjadi

Memprediksi profil kecepatan lapisan batas laminar tanpa gradient tekanan

Solusi exact (Metode Blausius)

Fungsi aliran ψ untuk mengurangi variable-variabel bergantung u dan v ke dalam satu nama ψ . Kita masukkan ke dalam persamaan momentum di atas

Diubah ke dalam persamaan diferensial biasa dengan perubahan-perubahan variable:

Setelah beberapa manipulasi turunan parsial, substitusikan

Dan

Kondisi batas untuk ini adalah

Solusi persamaan di atas harus dilakukan secara numeric

Solusi masalah-masalah Blausius seperti table di bawah ini

Komponen u bertambah dari nol pada dinding (η=0) sampai 99% dari u_∞ pada η=4.92

Ketebalan lapisan batas

u(x,y) adalah suatu fungsi η

Substitusikan dalam .

Hasilnya adalah

Profil kecepatan memiliki bentuk yang sama terhadap ketebalan lapisan batas pada setiap daerah x atau dengan kata lain profil kecepatan sama pada masing-masing daerah.

Metode integral momentum

Kita integralkan persamaan konservasi momentum di atas di mana tidak ada gradient tekanan (dp/dx=0).

Pada y=δ , u dapat diperkirakan sebagai nilai aliran bebas , u_∞

Persamaan kontuinitas dapat diintegralkan menjadi

Kalikan dengan u_∞

Persamaannya menjadi

Tegangan geser pada dinding hanya terdapat pada arah sumbu x saja.

Persamaan di atas menunjukkan konservasi momentum linear dalam bentuk integral. Ini menunjukkan laju kerugian momentum disebabkan oleh gaya geser oleh dinding. Dengan menggunakan metode integral, persamaan nondimensional adalah

Cf adalah koefisien gesek kulit.

Kemudian kita menebak solusi dalam bentuk persamaan u/ u_∞= fn(y/ δ). Tebakan dibuat dengan memenuhi empat hal yang benar dari profil kecepatan:

Sehingga

Jika fungsi fn(y/ δ) ditulis sebagai polynomial dengan empat konstanta a, b, c, dan d didalamnya.

Empat hal yang diketahui tentang profil diberikan

0=a
1=0+b+c+d
0=b+2c+3d
0=2c

Persamaannya menjadi

Perkiraaan profil kecepatan dibandingkan dengan profil Blausius exact. Keduanya sama-sama memiliki error maksimum tidak lebih dari 8%.

Untuk menghitung , kita substitusikan

di dalam

kemudian kita integralkan menjadi

atau

Kita integralkan menggunakan kondisi batas δ²=0 pada x=0

atau

Analogi perpindahan panas dan momentum
Anggap sebuah lapisan batas di dalam fluida dengan temperatur bulk , mengalir pada sebuah plat datar dengan temperatur Tw, persamaan momentum dengan kondisi batasnya adalah

Persamaan energi dapat ditulis di dalam konsep temperatur

sebagai

Prediksi profil kecepatan dan temperatur adalah identik. Jika v dan alpha adalah sama, maka distribusi temperatur di dalam lapisan batas adalah

Kita dengan segera dapat mencari koefisien perpindahan panas dengan menggunakan persamaan

Koefisien perpindahan panas untuk aliran laminar,incompressible melalui sebuah plat

Persamaan energy adalah

Kita integralkan persamaan di atas

Kita evaluasi v pada y=δt, menggunakan persamaan kontuinitas

persamaan di atas menjadi

Persamaan di atas menunjukkan konservasi energy panas di dalam bentuk integral, bahwa laju energy panas dibawa oleh lapisan batas sesuai dengan laju panas yang masuk ke dinding.

Distribusi temperature di dalam lapisan batas laminar

Distribusi temperature adalah T_∞ untuk > δt . Kondisi ini menetapkan dT/dy sama dengan nol pada y=δt . Kondisi keempat bentuk persamaan

pada dinding di mana u=v=0.

Perkiraan profil temperature dengan sebuah fungsi kubik

Substitusikan persamaan-persamaan di atas, dan kita dapatkan

Sehigga profil temperature adalah

Simulasi CFD pada Software CFDSOF

Langkah-langkah simulasi CFD aliran laminar melewati sebuah plat datar adalah sbb:
1. Menentukan daerah domain p x l x t = 1 x 0.1 x 1m. Dengan jumlah cell 50i x 20 j

2. Menentukkan daerah inlet 1 (i1,j2 sampai i1,129), daerah inlet 2 (i50,j2 sampai i5019j29), daerah wall (i1,j1 sampai i50,j1), dan daerah simetri (i1,j20 sampai i50,j20)

Domain

3. Menentukan konstanta fisikal yaitu densitas = 1000 kg/m3 dan dinamik viskositas = 9E-4 kg/ms.

4. Menentukan kondisi sempadan inlet 1 dengan nilai kecepatan u=0.001m/s dan inlet 2 sebagai pressure inlet.

5. Lakukan iterasi

6. Kita bisa lihat Kontur kecepatan u dan nilai kecepatan u pada setiap titik nodal i.

Kontur kecepatan u

Membuat Program Profil Kecepatan di Visual Basic

Setelah mendapatkan data dari hasil simulasi CFD, kemudian kita membuat program di dalam VBA untuk mendapatkan hasil profil kecepatan.

Pertama-tama kita mencari kinematic viskositas dahulu. Setelah kita mendapatkan kinematic viskositas maka kita akan mendapatkan bilangan Reynolds

Metode Blausius

Dari persamaan

Setelah itu,kita membuat coding pada VBA. Langkah pertama adalah kita memasukkan hasil kecepatan u di setiap titik nodal pada worksheet yang tersedia. Data yang akan kita cari adalah u/u∞, y/δ, y, dan δ. Titik nodal yang akan kita amati adalah pada i=1,5,9,13,17,21,25,29,33,37,41,45,dan 49. Kita cantumkan juga tombol perintah untuk melakukan perhitungan.

Coding pada VBA adalah seperti gambar berikut di bawah.

Coding terus berulang dari titik nodal i=1 sampai i=49. Setelah selesai membuat coding, kemudian kita tekan tombol perintah "Hitung". Dan kita dapatkan hasil data-data seperti gambar di bawah ini.