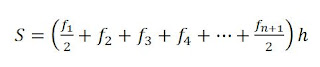Metode Bisection (Komputasi Teknik)

Contoh persamaan f(x)= x^3 - x - 1
Carilah akar persamaannya dengan metode bisection

Jawab
Pertama-tama kita masukkan range untuk x1 dan x2 yaitu 0 dan 2 pada worksheet di excell
Lalu buat module untuk perhitungannya

Kita masukkan fungsi xm (x1,x2)
xm adalah nilai tengah antara x1 dan x2
Syarat bisection adalah tanda y1 berbeda dengan tanda y2
xm = (x1 + x2) / 2

masukkan nilai x1 pada y1
jika y1*ym negatif, maka x2=xm
jika sebaliknya, maka x1=xm

Lakukan looping sampai error <0.0000001

HAsilnya ketika dirunning

Metode Iterasi (Komputasi Teknik)

Banyak persamaan matematika yang dapat diselesaikan secara exact tetapi jauh lebih banyak lagi yang hanya dapat diselesaikan dengan metode numeric.

Istilah `` iteratif'' metode mengacu pada berbagai teknik yang menggunakan aproksimasi untuk mendapatkan solusi yang lebih akurat untuk sistem linier di setiap langkah. 

Untuk mencari solusi dari persamaan f(x) = 0 digunakan sejumlah proses trial dan error yang sering juga disebut metode iterasi.

Solusi dari persamaan di atas disebut akar persamaan f(x)=0

Ada beberapa tipe metode iterasi yaitu:

1. Metode Bisection

Metode bisection sangat sederhana dan dapat diandalkan. Metode ini sering digunakan untuk mendapatkan pendekatan kasar solusi yang kemudian digunakan sebagai titik awal untuk metode yang lebih cepat konvergen. Metode dijamin konvergen ke akar dari fungsi f jika fungsi f kontinu pada interval (a,b). Fungsi f(a) dan f(b) memiliki tanda yang berlawanan. Absolte error dibelah dua pada setiap langkah iterasi sehingga metode akan konvergen secara linear yang relatif lambat. Jika p1 = (a + b) / 2 adalah titik tengah dari interval awal, dan pn adalah titik tengah interval pada langkah ke-n, maka perbedaan antara pn dan solusi p dibatasi.

Algoritmanya sebagai berikut

INPUT: Function f, endpoint values a, b, tolerance TOL, maximum iterations NMAX

CONDITIONS: a < b, either f(a) < 0 and f(b) > 0 or f(a) > 0 and f(b) < 0

OUTPUT: value which differs from a root of f(x)=0 by less than TOL

N ← 1

While N ≤ NMAX { limit iterations to prevent infinite loop

  c ← (a + b)/2 new midpoint

  If (f(c) = 0 or (b – a)/2 < TOL then { solution found

    Output(c)

    Stop

  }

  N ← N + 1 increment step counter

  If sign(f(c)) = sign(f(a)) then a ← c else b ← c new interval

}

Output("Method failed.") max number of steps exceede

2. Metode False Position

Metode bisection menjamin konvergensi pada akarnya tetapi relative lambat dan sulit untuk diaplikasikan untuk system persamaan non linear dua atau lebih. Metode false position merupakan salah satu cara untuk mengatasi hal ini. Kita mulai dengan melokasikan interval mula-mula (x₁,x₂), dan diasumsikan fungsi berubah tanda hanya sekali di dalam interval ini. Sekarang kita mendapatkan x₃ di dalam interval ini, yang didapat dari persimpangan antara sumbu x dan garis lurus melalui (x₁,f(x₁)) dan (x₂,f(x₂)).

Sekarang kita memilih interval yang baru dari dua pilihan (x1,x3) dan (x3,x2) tergantung di interval mana fungsi berubah tanda.

Metode false position berbeda dari metode bisection hanya di dalam pilihan pembagian interval pada masing-masing iterasi. Metode ini lebih cepat konvergen ke akar karena merupakan algoritma yang menggunakan bobot yang sesuai dari ujung mula titik x1 dan x2 dengan menggunakan informasi tentang fungsi, atau data dari masalah. Dengan kata lain, mencari x3 adalah prosedur statis dalam kasus metode bisection karena untuk x1 dan x2 yang diberikan, ini memberikan x3 yang identik, tidak peduli apa fungsi kita ingin memecahkan. Di sisi lain, metode false position menggunakan informasi tentang fungsi untuk mendapatkan di x3.

3. Metode Newton Raphson

Metode Newton-Raphson adalah suatu metode iterasi untuk menyelesaikan persamaan f(x)=0, di mana f diasumsikan mempunyai turunan kontinu f’.

Metode ini secara umum digunakan karena sederhana dan cepat.

Idenya adalah memperkirakan grafik f dengan tangent yang cocok.

Menggunakan nilai x₀ didapat dari grafik f, x₁ adalah titik persimpangan dari sumbu x dan tangent kurva f pada x₀. Maka

Langkah kedua kita menghitung x₂ = x₁ – f(x₁)/f’(x₁), langkah ketiga diulang lagi x₃ dari x₂ menggunakan rumus yang sama. 

Algoritmanya adalah

Jika terjadi f’(x_n) = 0 untuk beberapa n (lihat algoritma baris 2) ,lalu mulai lagi dengan nilai tebakan baru x₀.

Pada baris 4 adalah criteria terminasi. Jika urutan x_n konvergen dan memenuhi criteria, kita mendapatkan hasil yang akurat.

4. Metode Secant

    Metode ini menggunakan garis perkiraan berdasarkan interpolasi. Kita asumsikan mempunyai perkiraan dua akar α, katakanlah x₀ dan x₁. Kemudian kita menghasilkan sebuah fungsi linear

Garis ini sering disebut garis secant.  Persamaannya adalah

i

Ini linear dalam x; dan dengan evaluasi arah, ini memenuhi kondisi interpolasi. Kita sekarang menyelesaikan persamaan q(x)=0 , ditandai dengan akar x₂. 

Kita sekarang dapat mengulangi proses tersebut. Gunakan x₁ dan x₂ untuk membuat garis secant yang lainnya

Hal mendasar perbandingan dari beberapa metode iterasi di atas adalah:

1. Laju konvergensi

2. Jumlah usaha komputer setiap iterasi

3. Sensitivitas metode terhadap nilai awal dan nilai tengah

Metode Bisection : 

- urutan konvergensi : satu bit per iterasi

- Evaluasi fungsi per iterasi : 1

- Kehandalan konvergensi : dijamin konvergen

Metode False Position: 

- urutan konvergensi : satu bit per iterasi

- Evaluasi fungsi per iterasi : 1

- Kehandalan konvergensi : dijamin konvergen

Metode Newton Raphson: 

- urutan konvergensi : dua bit per iterasi

- Evaluasi fungsi per iterasi : 2

- Kehandalan konvergensi : ssensitif terhadap nilai awal.Akan konvergen dengan cepat jika dekat akar

Metode Secant: 

- urutan konvergensi : 1.62 bit per iterasi

- Evaluasi fungsi per iterasi : 1

- Kehandalan konvergensi : tidak dijamin konvergen jika tidak dekat dengan akar. Metode ekonomis

Iterasi menggunakan metode Newton-Raphson (Komputasi Teknik)

Metode Newton-Raphson adalah suatu metode iterasi untuk menyelesaikan persamaan f(x)=0, di mana f diasumsikan mempunyai turunan kontinu f’.

Metode ini secara umum digunakan karena sederhana dan cepat.

Idenya adalah memperkirakan grafik f dengan tangent yang cocok.

Menggunakan nilai x₀ didapat dari grafik f, x₁ adalah titik persimpangan dari sumbu x dan tangent kurva f pada x₀. Maka

Langkah kedua kita menghitung x₂ = x₁ – f(x₁)/f’(x₁), langkah ketiga diulang lagi x₃ dari x₂ menggunakan rumus yang sama. 

Algoritmanya adalah

Jika terjadi f’(x_n) = 0 untuk beberapa n (lihat algoritma baris 2) ,lalu mulai lagi dengan nilai tebakan baru x₀.

Pada baris 4 adalah criteria terminasi. Jika urutan x_n konvergen dan memenuhi criteria, kita mendapatkan hasil yang akurat.

Sumber : Advanced Engineering Mathematics_Kreyszig 9th   

Contoh :

Cari akar persamaan dari f(x) = x³ + x -1 = 0

Maka   f’(x) = 3x² + 1

            x_n+1 = x_n – ((x_n³ + x_n - 1) /  (3x_n² + 1)) = (2x_n³ + 1) / (3x_n² + 1)

Coding nya seperti di bawah ini

Setelah di running 

Hasilnya masih salah, saya akan perbaiki di lain kesempatan

Bersambung....

Mesh study on two parallel plates - case (Aplikasi CFD)

Terdapat dua plat yang sejajar dengan jarak H=0,1 m  dan dengan panjang L=1m, lalu dialirkan udara (laminer) dengan densitas r=1,2 kg/m³.

Terdapat 2 Kasus yang terdapat dalam contoh ini

Yaitu dengan mengganti salah satu parameter : 

1.  Mengganti viskositas m=4x10^-5 kg/m.s dan m= 10^-5 kg/m.s dengan menetapkan kecepatan inlet u_inlet=0,01m/s.
2.  Mengganti kecepatan inlet u_inlet=0,01m/s dan u_inlet=0,04m/s dengan menetapkan viskositas m=4x10^-5 kg/m.s

Cari dan analisis dengan menggunakan CFDSOF untuk kedua kasus diatas

Sama seperti posting saya sebelumnya, hanya saja terdapat perbedaan pada variabel-variabel yang dirubah dan penerapan mesh study / grid dependency test.

Seperti yang kita ketahui, Grid yang baik adalah grid yang bisa mengakomodir peristiwa aliran dalam ruang dan waktu.

Pada lapisan batas terjadi gradien kecepatan yang besar dibandingkan pada area yang lainnya maka dibuat grid yang lebih rapat.

Mesh study diperlukan untuk memperkecil error pada saat iterasi untuk mencapai solusi yang konvergen sehingga tercapai hasil yang lebih baik.

Adapun langkah-langlah pada software CFDSOF sbb:

Variabel viskositas m=4x10^-5 kg/m.s dan u_inlet=0,01m/s

1. Input alokasi memori

2. Menentukan domain dengan p x l x t = 1 x 0.1 x 1. Pada arah i = 50 cell, dan arah j = 30

3. Pilih menu bangun grid pada arah x. Kemudian inisialisasi segmen. Kita membagi panjang (arah x) menjadi dua segmen sama panjang. Segmen 1 berisi 28 cell dan segmen 2 berisi 20 cell

4. Kita memilih modifikasi segmen untuk mengatur kerapatan sehingga di dekat lapisan batas terdapat grid yang lebih rapat. Kita tentukan faktor pemberat 3

5. Sekarang kita akan membangun grid pada arah y. Kemudian inisialisasi segmen. Kita membagi tinggi (arah y) menjadi tiga segmen. Segmen 1 dari y=0 sampai y=0.025, segmen 2 dari y=0.025 sampai y=0.75, dan segmen 3 dari y=0.075 sampai y=0.1. Segmen 1 berisi 10 cell, segmen 2 berisi 8cell, dan segmen 3 berisi 10 cell

 

6. Modifikasi segmen pada segmen 1 dan 3 dengan faktor pemberat 4. Pada segmen 1 masukkan faktor pemberat pada titik awal sedangkan pada segmen 3 masukkan faktor pemberat pada titik akhir.

7. Atur cell, inlet 1 pada i1,j2 - j29 dan inlet 2 i50,j2-j29.

8, Menentukkan konstanta fisikal r=1,2 kg/m³ viskositas m=4x10^-5 kg/m.s. 

9. Menentukkan kondisi sempadan, inlet 1 kecepatan u = 0.01 m/s dan inlet 2 tekanan

10. Melakukan iterasi

11. Adapun grafik hasil grid, kontur tekanan, kontur kecepatan, dan plot xy seperti gambar di bawah ini

Hasil Grid

Kontur Kecepatan

Kontur tekanan

Plot XY

Variabel viskositas m=10^-5 kg/m.s dan u_inlet=0,01m/s

Langkah-langkah di dalam CFDSOF sama dengan di atas hanya ada beberapa perubahan, Sebelumnya lakukan dulu reset data sehingga dapat kembali dilakukan iterasi.

Pada menu konstanta fisikal , masukkan viskositas 1e-5.

Adapun hasil grafiknya

Kontur kecepatan

Kontur tekanan

Variabel viskositas m=4 x 10^-5 kg/m.s dan u_inlet=0,04m/s

Kita ganti konstanta fisikal viskositas m=4 x 10^-5 kg/m.s dan kondisi sempadan pada inlet 1  u_inlet=0,04m/s

Hasil grafiknya seperti berikut

Kontur kecepatan

Kontur tekanan

Grafik kontur kecepatan berdasarkan besarnya kecepatan pada berbagai kondisi parameter adalah sebagai berikut :

Kontur kecepatan. u_inlet=0,01m/s , m=4x10^-5 kg/m.s  

Kontur kecepatan. u_inlet=0,01m/s , m=10^-5 kg/m.s

Kontur kecepatan. u_inlet=0,04m/s , m=4x10^-5 kg/m.s

Dilihat dari grafik kontur kecepatan di atas, 

Untuk kasus 1: viskositas m=4x10^-5 kg/m.s dan m= 10^-5 kg/m.s dengan menetapkan kecepatan inlet u_inlet=0,01m/s. Kita kembali mengacu pada persamaan momentum arah-x 2D adalah 

Gaya inersia yang terjadi adalah sama, perbedaan yang terjadi adalah pada gaya gesek akibat perbedaan viskositas. Kondisi dengan viskositas yang lebih tinggi menyebabkan gaya gesek yang lebih tinggi. Gaya gesek yang lebih tinggi menghambat momentum yang terjadi akibatnya aliran berkembang penuh pada jarak yang lebih pendek.

Untuk kasus 2: kecepatan inlet u_inlet=0,01m/s dan u_inlet=0,04m/s dengan menetapkan viskositas m=4x10^-5 kg/m.s.

Pada kondisi ini, kecepatan yang lebih tinggi menyebabkan gaya inersia yang lebih tinggi, sedangkan viskositasnya tetap. Gaya inersia yang lebih tinggi memaksakkan gesekan yang lebih rendah karena tegangan geser pada dinding lebih rendah yang menghambat aliran fluida.

Satu parameter non dimensional yang penting untuk memaparkan karakteristik aliran adalah bilangan Reynolds (Re), yang mendefinisikan ratio antara gaya inersia atas gaya gesek.

Daerah hydrodynamic entry region akan sama jika bilangan Reynolds (Re) sama. 

Integrasi Numerik - Case (Komputasi Teknik)

Integrasikan fungsi table di bawah ini dengan menggunakan Trapezoidal Rule dan Simpson’s Rule.

Fungsi di atas ditabulasikan pada 10 titik.

Trapezoidal Rule

Integrasi untuk fungsi diatas dengan menggunakan metode Trapezoidal Rule adalah

Terima kasih atas pencerahan dari teman saya Hasnan sehingga saya mendapat informasi untuk membuat program VBA dengan menggunakan worksheet di Excel.

Pertama-tama kita masukkan nilai-nilai x dan f(x) pada worksheet di Excel.

Kemudian kita membuat command button untuk mengeksekusi jalannya program. Kita pilih Developer pada menubar, pilih design mode, kemudian pilih insert command button. Untuk merubah tampilan nama pada command button kita pilih caption dan silahkan merubahnya sesuai keinginan .

Setelah itu double klik pada command button untuk menulis coding 

Coding nya seperti di bawah ini

Pertama-tama kita deklarasikan h dan s seperti gambar di atas.

Kemudian kita menghitung h = (x10 s/d x1) / 9 .

Kembali kita lihat mencari rumus s di atas,maka kita definisikan s untuk x1. 

Setelah itu kita lakukan Looping untuk x2 sampai x9. Nilai s yang baru didapat dari nilai s1 dijumlahkan secara looping sampai s9.

Setelah selesai looping, kita tambahkan lagi untuk s10.

Nilai akhir s kita tampilkan pada worksheet (cell (7,3).

Adapun hasil perhitungan seperti gambar di bawah ini.

Simpson's Rule

Rumus untuk mencari integrasi numerik dengan metode Simpson's Rule adalah

Simpson's Rule memerlukan titik-titik ganjil. Kita akan memakai Trapezoidal Rule untuk dua titik pertama dan menggunakan Simpson's Rule pada titik-titik sisanya

Perhitungannya adalah

Coding nya seperti di bawah ini

Untuk dua titik pertama yaitu untuk x1 dan x2, kita memakai trapezoid rule
Untuk x2 sampai x10,dipakai simpson rule dengan penjumlahan hasil dari trapezoid rule.

Setelah running program,maka hasilnya akan seperti gambar di bawah.