Persamaan pada kondisi-kondisi sempadan adalah φ0 = 1 pada x = 0 dan φL = 0 pada x = L. Panjang L = 1.0m. Temperatur pada x=0 adalah 274K dan pada x=L adalah 273K. Menggunakan lima cell yang sama dan central differencing scheme untuk konveksi dan difusi, simulasikan distribusi dari φ sebagai fungsi dari x untuk :
case 1 : u= 0.1 m/s , ρ=0.1 kg/m3
case 2 : u= 0.1 m/s , ρ=0.01 kg/m3
case 3 : u= 0.1 m/s , ρ=0.001 kg/m3
Simulasi pada software CFDSOF adalah sbb:
Case 1
1. Input alokasi memori pada software CFDSOF
2. Input domain dengan p x l x t = 1 x 0,1 x 1 . Pada arah x, cell dibagi menjadi 7 sedangkan arah y cell dibagi menjadi 3
3. Input model untuk menghitung temperatur dan wall konduktif
4. Mengatur cell
5. Mengatur kondisi sempadan pada wall 1 dan wall 2: Temperatur pada wall 1 dan wall 2 adalah 274K dan 273K.
6. Memasukkan nilai densitas pada kondisi fisikal : densitas = 0.1 kg/m3
7. Masuk pada menu olah kontrol persamaan dan pilih propert/temperatur entalpi.
8. Masuk pada menu mahir dan pilih pakai variable tetap. Kemudian set nilai tetap kecepatan u = 0.1 m/s.
9. Melakukan iterasi
10. Melihat hasil grafik kontur temperatur dan plot xy (panjang vs temperatur)
 |
| Grafik kontur temperatur case 1 |
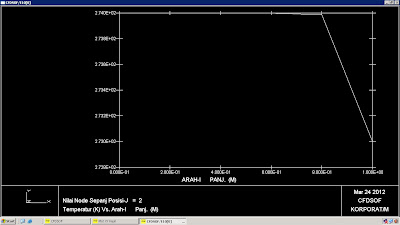 |
| Grafik plot xy case 1 (panjang vs temperatur) |
Langkah-langkah untuk case 2 dan case 3 sama seperti langkah-langkah di atas hanya saja kita ganti nilai densitas dari kondisi fisikalnya.
Case 2
Mengganti nilai densitas pada kondisi fisikal. ρ = 0.01 kg/m3.
Hasil grafik kontur temperatur dan plot xy ( panjang vs temperatur) adalah seperti di bawah ini
 |
| Grafik kontur temperatur case 2 |
 |
| Grafik plot xy case 2 (panjang vs temperatur) |
Case 3
Mengganti nilai densitas pada kondisi fisikal. ρ = 0.001 kg/m3.
Sehingga grafik kontur temperatur dan plot xy (panjang vs temperatur) adalah seperti di bawah ini
 |
| Grafik kontur temperatur case 3 |
 |
| Grafik plot xy case 3 (panjang vs temperatur) |
Rumus untuk mencari konveksi massa flux per satuan luas adalah
F = ρ u
dan untuk mencari difusi konduktansi pada permukaan cell adalah
D = Γ / δx
Konveksi massa flux berbanding lurus dengan perkalian antara densitas dan kecepatan fluida. Pada case 1,2,dan 3 kecepatan fluidanya tetap yaitu 0.1 m/s sedangkan densitasnya berbeda-beda. Pada case 1,2,dan 3 densitasnya berturut-turut adalah 0.1 kg/m3, 0.01 kg/m3, dan 0.001 kg/m3.
Dapat dilihat dari grafik plot xy case 2 dan case 3, fenomena yang terjadi adalah penurunan konveksi massa flux karena nilai densitas yang berkurang. Pada grafik plot xy case 3, konveksi massa flux sangat kecil dan fenomena yang terjadi pada case 3 adalah difusi.
F = ρ u
dan untuk mencari difusi konduktansi pada permukaan cell adalah
D = Γ / δx
Konveksi massa flux berbanding lurus dengan perkalian antara densitas dan kecepatan fluida. Pada case 1,2,dan 3 kecepatan fluidanya tetap yaitu 0.1 m/s sedangkan densitasnya berbeda-beda. Pada case 1,2,dan 3 densitasnya berturut-turut adalah 0.1 kg/m3, 0.01 kg/m3, dan 0.001 kg/m3.
Dapat dilihat dari grafik plot xy case 2 dan case 3, fenomena yang terjadi adalah penurunan konveksi massa flux karena nilai densitas yang berkurang. Pada grafik plot xy case 3, konveksi massa flux sangat kecil dan fenomena yang terjadi pada case 3 adalah difusi.













No comments:
Post a Comment